Beim Schnitzen eines Bogens bedarf es größter Sorgfalt, damit die querschnittsbegrenzende Jahrringoberfläche im Bereich der Zugzone nicht verletzt, d.h. angeschnitten wird. Unter der Voraussetzung darf an der Zugzonenberandung von einem nahezu unbeschädigten Faserzustand ausgegangen werden. Für die weiteren Betrachtungen des Leistungspotenzials eines Bogens werden daher die mechanischen Kenngrößen für das sogenannte »Clear-Wood« herangezogen. Im Falle des vorliegenden Eibenbogens sind die in der Randspalte angeführten Kenngrößen (gemäß Literatur) maßgebend.
Bei den Tabellenwerten handelt es sich um ermittelte Werte aus statischen Versuchen, welche aufgrund der kurzzeitigen Belastung eines Bogens zum Zeitpunkt der Maximalbeanspruchung - das ist der Moment des Abschusses eines Pfeiles - um rund 10 bis 15 Prozent erhöht werden dürfen.
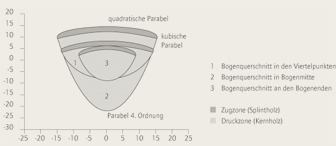
Beim vorliegenden Eibenbogen sind die Querschnitte derart geformt, dass die außenliegende Zugseite genau der Jahrringstruktur folgt, wogegen die innenliegende Druckseite eher einen »bauchigen« Verlauf aufweist. Das im Vergleich zum rötlichen Kernholz auf Zug höher belastbare helle Splintholz bildet die Zugzone und das Kernholz die Druckzone im Bogenquerschnitt. Die mathematische Beschreibung der Querschnittsberandung erfolgt mit ganzrationalen Polynomen, wobei der Zugbereich durch eine Parabel und der Druckbereich durch ein Polynom 4. Grades angenähert wird. Für den Übergangsbereich zwischen der Zug- und Druckzone wird eine kubische Parabel für die Approximation (Abb. 1) gewählt.
Die spannungsfreie Form eines fertigen Bogens ist in etwa gerade, wobei die Ausgangsform vom Faserverlauf abhängt und daher von Bogen zu Bogen unterschiedlich ist.Der dieser Berechnung zugrundegelegte Eibenbogen weist in der spannungsfreien Geometrie bereits einen Stich von rund 55mm auf, was auf oftmaligen Gebrauch zurückgeführt werden kann. Bei jedem Spannvorgang wird der Bogen nämlich an die Grenze seiner Tragfähigkeit gebracht, womit eine »Materialermüdung« und somit eine Reduktion des Elastizitätsmoduls einhergeht. Für die Berechnung wurde daher nicht der in der Tabelle für »fehlerfreie« Kleinproben angegebene Biegeelastizitätsmodul von 15.700N/mm², sondern ein den Versuchen angepasster Wert von 12.000N/mm² gewählt. Die Ermittlung der Schnittgrößen im Bogen erfolgt auf Basis einer geometrisch nicht linearen Berechnung (GNL) mit großen Verschiebungen und moderaten Rotationen.
Dazu ist die Kenntnis des vorgespannten Gleichgewichtszustandes notwendig. Dieser spannungsbehaftete Ausgangszustand wird erreicht, indem dem spannungsfreien Bogen ein Stichzuwachs von 55mm auf 194mm aufgezwungen und der Bogensehne die Zugkraft als vorgegebene Vorspannkraft eingeprägt wird. Diese Vorspannkraft kann im Versuch über eine Kraftmessdose bestimmt werden. Ausgehend von diesem Gleichgewichtszustand wird eine äußere Spannkraft auf das System Bogen-Sehne in der Mitte der Sehne aufgebracht. Die Reaktionskraft wird in der Bogenmitte als »Lagerkraft« durch den jeweiligen Benutzer des Bogens »abgenommen«. Die sich aus der Berechnung ergebenden Spannungen werden für die außenliegende Zugseite und die innenliegende Druckseite für den gespannten Grundzustand und den gezogenen Zustand (45cm Auszug, bezogen auf den gespannten Grundzustand) dargestellt.
Betrachtet man den gezogenen Zustand des Bogens und den damit zusammenhängenden Spannungszustand, so ist aus dem Diagramm leicht erkennbar, dass kurz vor dem Abschuss des Pfeiles der Bogen sowohl in der Zug- als auch in der Druckzone einem Spannungszustand ausgesetzt ist, welcher im Bruchbereich des »fehlerfreien« Eibenholzes liegt (errechnete maximale Zugspannungen: von 52N/mm² (Grundzustand) bis 104 N/mm² (gezogener Zustand), errechnete maximale Druckspannung: 63N/mm² (Grundzustand) bis 125N/mm² (gezogener Zustand). (Abb. 2)
Während zwischen dem Auszug des Bogens und der dazu notwendigen Kraft fast ein linearer Zusammenhang gegeben ist, ist ein ausgeprägter nichtlinearer Zusammenhang zwischen der Sehnenkraft und dem Bogenauszug gegeben. Diese Zusammenhänge wurden versuchstechnisch überprüft und bestätigt. (Abb. 3)
Die durch das Spannen des Bogens aufgewendete Arbeit wird in Form der inneren Verzerrungsenergie gespeichert. Diese gespeicherte Energie wird beim Loslassen der Bogensehne zum überwiegenden Teil in die kinetische Energie - Bewegungsenergie - des Pfeiles umgesetzt. Geringe Anteile gehen als kinetische Energie an die Sehne und den Bogen verloren. Werden diese Anteile näherungsweise vernachlässigt, so ergibt sich mit dem gemessenen Pfeilgewicht von 27,6g bei einem Pfeilauszug von 45cm (bezogen auf den gespannten Grundzustand) und der zugehörigen Kraft von 156N (entspricht einer Masse von rund 16kg) eine rechnerische Abfluggeschwindigkeit von rund 180km/h, wobei hier noch einmal darauf hingewiesen werden soll, dass dieser speziell berechnete Eibenbogen bereits einiges von der ursprünglichen Spannkraft verloren hat. Der Nachbau eines Wikingerbogens - ebenfalls aus Eibe - ergab (gemäß Literatur) für einen 20g schweren Pfeil eine gemessene Anfangsgeschwindigkeit von rund 200km/h.
Der im vorliegenden Beitrag untersuchte Eibenbogen wurde von Gerhard Schickhofer im Rahmen eines Bogenbaukurses unter Anleitung von Micha Wolf (siehe vorige Doppelseite) eigenhändig geschnitzt.
Mechanische Eigenschaften von Eibenholz für statische Beanspruchungen
Biegeelastizitätsmodul E||
15.700 N/mm²
Druckfestigkeit ‚D||
57 N/mm²
Zugfestigkeit ‚Z||
108 N/mm²
Biegefestigkeit ‚B||
85 N/mm²
Härte nach Brinell
HB|| 70 N/mm²
HB/ 30 N/mm²
Dimensions- und Formstabilität sehr gut
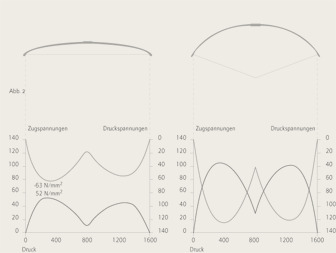
Abb. 2
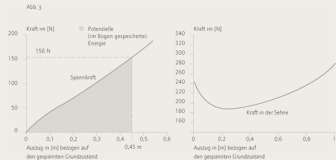
Abb. 3
